Hypothesetoetsen zijn statistische methodes om effecten (zoals statistische relaties op basis van een steekproef) te toetsen op lange-termijn-waarschijnlijkheid (significantie). Als het goed is, wordt hierbij ook altijd de praktische relevantie (sterkte) meegenomen.
Doelen van hypothesetoetsen
- Grondoorzaken valideren (Y=F(X)) in de analysefase (DMAIC)
- Na invoering van verbeteringen, deze ook toetsen op significantie (DMAIC)
Toelichting
Hypothesetoetsen kun je altijd inzetten indien er sprake is van twist, twijfel en/ of grote gevolgen. Algemeen geldt hier: bewijs dat een effect niet alleen geldt als aanname (op basis van gevoel of een steekproef), maar juist ook voor de langere termijn (populatie). Dit alles op basis van kansberekening (significantie) en (uiteindelijk) praktische relevantie.
Belangrijke hypothesetoetsen zijn rondom het begin van de vorige eeuw ontstaan (Pearson zijn correlatie ρ (1897) en Chi2-toets (1900); Gosset zijn Student’s t-test (1908); Fisher met zijn ANOVA en DOE, etc.), en hebben in de twintigste eeuw een enorme vlucht genomen. En niet alleen in de (academische) wetenschap, ook in toporganisaties binnen bijvoorbeeld de Automotive tot en met vele overheidsinstanties. En dus ook al vele decennia binnen de wereld van het verbeteren van organisaties, processen en afdelingen.
Met steeds snellere computers zijn kansberekeningen anno nu een ‘fluitje van een cent’ geworden. Wat rekenkracht betreft.
De Aanpak hierna slaat voornamelijk op de analysefase in DMAIC. Ofwel, is er sprake van géén relatie tussen Y en X (H0) versus wel een Y-X relatie (Ha). Desalniettemin zijn de vier stappen om een hypothese te toetsen in de hierop volgende Aanpak ook ‘breder’ in te zetten.
Zoals bijvoorbeeld het toetsen van kansverdelingen op Normaliteit, en of er sprake is van identieke variatie per categorie (beiden zijn aannames bij ANOVA). Bij de eerste stap dien je bijvoorbeeld de hypothesen wel anders te formuleren. En bij stap vier heb je met een andere interpretatie van doen.
Hypothesetoetsen aanpak
Stel hypothesen op. Formuleer je probleem in stellingen (‘hypothesen’). Het ‘onschuldige’ uitgangspunt heet de zogenaamde nulhypothese (H0) versus de alternatieve hypothese (Ha of H1). Ga uit van α=0,05 (vuistregel binnen DMAIC).
-
H0: geen effect (Analyse: géén Y-X relatie) - Ha: wel een effect (Analyse: wel een Y-X relatie)
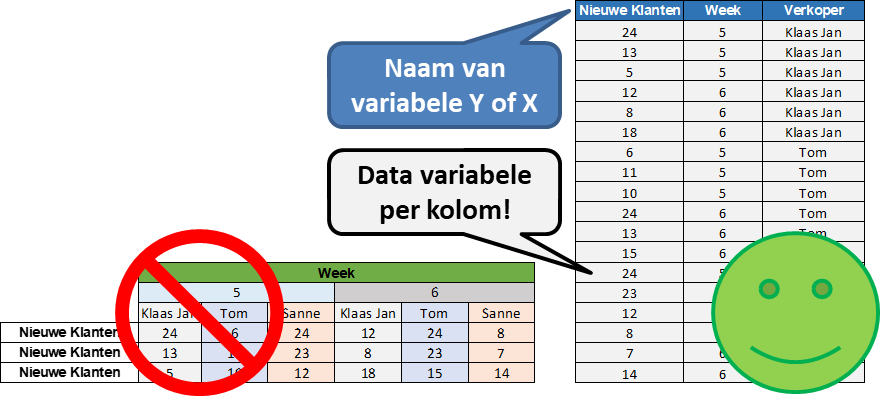
Visualiseer. Gebruik betrouwbare data (steekproef) om de relatie tussen een Y en X te visualiseren in een grafiek. Houd, bij het kiezen van de juiste grafiek, er rekening mee of Y en 
X continu of discreet zijn. Controleer ook nog op eventuele meetfouten.
Toets op significantie. Toets de Y-X relatie met behulp van een juiste hypothesetoets. Houd, bij het kiezen van de juiste toets, rekening met of data (Y en X) continu of discreet is. Indien de -bij een hypothesetoets altijd berekende- kans p kleiner is dan 0,05 … dan H0 verwerpen
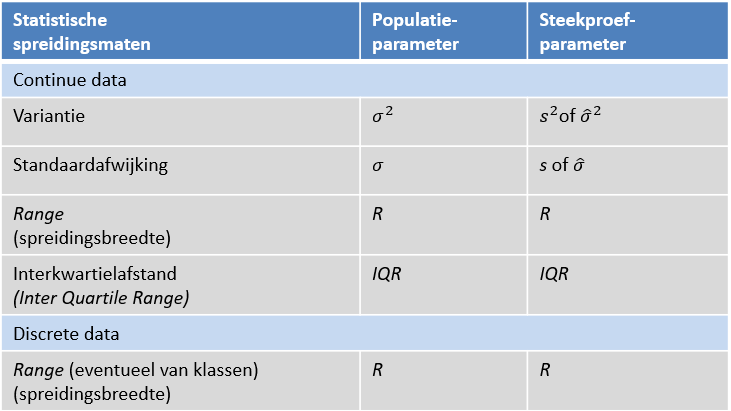
Bepaal de relevantie. Indien de relatie significant is, is deze relatie ook nog praktisch relevant? Bereken hiervoor statistieken die de sterkte bepalen, zoals de correlatie r (Y en X ‘continu’), de R2, of het verschil in 
gemiddeldes of medianen (X ‘discreet’). Interpreteer deze statistieken met inhoudelijke experts.
Duur van het uitvoeren van een hypothesetoets
Een hypothesetoets zelfstandig uitvoeren, is digitaal met statistische software in seconden tot minuten te doen. De interpretatie ervan met experts kan veel langer duren.
Synoniem en alternatief van een hypothesetoetsen
In het Engels: Hypothesis testing. Ook wel statistische toetsen genaamd.
Binnen web-marketing en startende organisaties (Lean Startup) wordt ook veel gerept over bijvoorbeeld A/B testing op basis van data. Bijvoorbeeld over verschillen in aantal leads per dag op een website. Dat blijft vaak bij het vergelijken van totalen of gemiddeldes. Statistische hypothesetoetsen ofwel kansberekeningen worden hierbij zelden gemaakt.
Voorbeelden van bekende hypothesetoetsen
Onderstaande tabel geeft bekende hypothesetoetsen weer. Deze toetsen zijn ingedeeld in enerzijds parametrische toetsen (Y is ‘redelijk’ normaal verdeeld) en verdelingsvrije toetsen (gaan uit van bijvoorbeeld discrete data of zijn robuuster voor scheve kansverdelingen, maar hebben vaak een iets grotere β-fout). In veel gevallen geven ze vergelijkbare p-waarden.
Klik op One-Way ANOVA en Regressieanalyse voor meer informatie over deze hypothesetoetsen.
