Hoofdstukken
Hypothesetoetsen: regressieanalyse | Lean Six Sigma Partners
Doel
• Een relatie tussen twee continue variabelen toetsen op significantie en sterkte
• Een (lineaire) regressielijn berekenen tussen Y en X, inclusief toetsing op significantie
In het kort
Regressieanalyse is een statistische methode, waarmee een relatie tussen twee continue variabelen wordt getoetst op wel/geen significantie. Deze relatie kan afwezig, deels aanwezig (lineair of niet-lineair) of (heel) sterk zijn.
Toelichting
Een regressieanalyse helpt om aannames (hypothesen) te bevestigen of te weerleggen.
De term regressie is misschien wat bijzonder (betekent letterlijk ‘teruggang’). Deze term is door Francis Galton bedacht bij onderzoek naar erfelijke eigenschappen. Hij introduceerde de rekenmethode ‘kleinste kwadratenmethode’ om tussen puntenparen de optimale regressielijn te krijgen (begin negentiende eeuw). Regressie-
analyse is nog verfijnd door Karl Pearson.
Meer te weten komen over Hypothesetoetsen? Klik dan hier en schrijf je in voor de Green Belt training.
De formule, die berekend (geschat) wordt door software, is: Y = a0 + a1*X + e, waarbij
• Y de onafhankelijke of te verbeteren continue variabele is
• X de afhankelijke, mogelijke (grond)oorzaak is
• e de error of residuwaarde ofwel het verschil tussen regressielijn en werkelijke waarde is
• a1 de zogeheten richtingscoëfficiënt of ‘helling’ is van de regressielijn, en
• a0 het intercept ofwel snijpunt is op de Y-as (de bias bij een MSA inzake accuraatheid)
 Aanpak
Aanpak
• Definieer probleem en doel. Stel de hierbij relevante hypothesen op (H0: de regressielijn is grofweg ‘horizontaal’, ofwel a1 = 0 versus Ha: a1 ≠ 0)
• Visualiseer de X-Y relatie met behulp van een spreidingsdiagram. Tip: meestal heb je (veel) meer dan 10 metingen nodig
• Zorg voor de executie van regressieanalyse tussen de Y en de X. Interpreteer de p-waarden en het (lineair) patroon in de grafiek. Is het verband statistisch significant?
• Indien significant: wat is de relevantie van de relatie? Interpreteer de sterkte door middel van de correlatie r of R2.
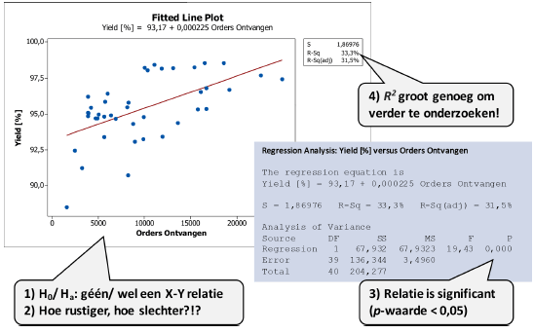
Binnen Minitab adviseren we om te werken met Fitted Line Plot. Hierin wordt zowel een spreidingsdiagram gemaakt, als de regressielijn met p-waarde en sterktes zoals een R2 samen berekend.
Synoniem en/of alternatief
In het Engels: Simple Linear Regression. Er bestaan diverse andere regressiemethoden, zoals meervoudige regressie (verklaar Y met meerdere X’en), niet-lineaire of robuuste regressie.
Duur
Een regressieanalyse maken is, met behulp van software, in enkele minuten te doen.
Voorbeeld
De wekelijkse Yield (% goed geleverd) is hier gerelateerd aan de hoeveelheid orders (drukte).