Een steekproef is een selectie van alle mogelijke metingen (populatie). Een steekproef neem je in de praktijk vaak om uitspraken te doen over de gehele populatie.
Toelichting
(1) Een steekproef is een selectie van alle mogelijke metingen (populatie). Een steekproef gebruik je in de praktijk vaak om uitspraken te doen over de gehele populatie. Bijvoorbeeld de exit polls bij verkiezingen, of een periode in de tijd in een proces.
(2) Een populatie is een complete, gedefinieerde groep eenheden waar je iets aan kunt meten. Bijvoorbeeld alle stemgerechtigde mannen in Nederland.
(3) Een proces is een verzameling tijdgerelateerde activiteiten (processtappen), om een stroom aan eenheden (diensten of producten) samen te stellen en te leveren aan (een) klant(en). Voorbeeld: het samenstellen van een leasecontract. Alle contracten die ooit zijn samengesteld in het proces vormen samen een populatie. Meet je de doorlooptijd van het opstellen van een leasecontract in de laatste maand , dan is dat een steekproef.
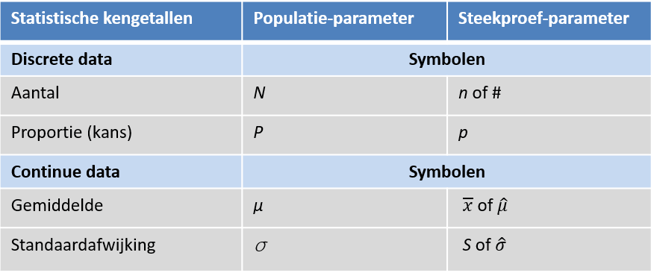
(4) Statistische symbolen per kengetal: zie onderstaande tabel.
Steekproef voorbeeld
Hieronder zie je een steekproef met 4 cirkels (1 zwarte, 3 grijze). De populatie (cirkel) is hier alle 28 cirkels (4 zwarte en 24 grijze).
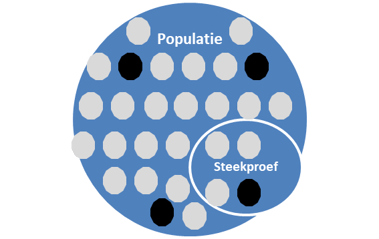
Noot: Om de hier geïntroduceerde basisbegrippen te verduidelijken laten we hier een ‘kleine’ populatie van slechts 28 cirkels zien. Niet ‘oneindig groot’, dus.
In de praktijk is de populatie meestal echter veel groter, tot wel (bij benadering) oneindig groot. Daar gaan we verder in dit boek dan ook van uit. Is dat in jouw verbetertraject niet het geval? Laat je dan adviseren door een ervaren en opgeleid persoon op dit gebied.
Steekproef vuistregels
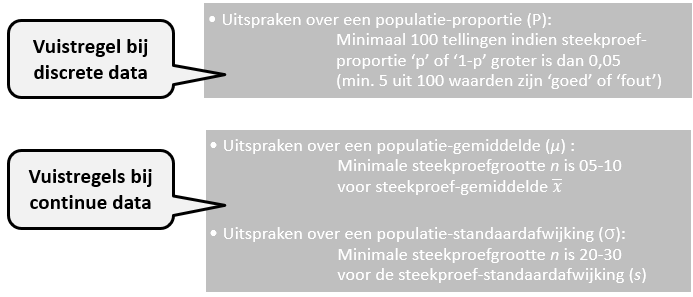
Er zijn vuistregels over hoe groot de minimale steekproefgrootte moet zijn, om vaak toch verantwoorde uitspraken te doen over de populatie. Aanname hierbij is dat de populatie ‘erg groot’ of bij benadering oneindig is. Verder zijn onderstaande vuistregels voor steekproefgroottes i.i.g. afhankelijk van type data (discreet of continu) en de statistische parameter.
Doelen van een steekproef
- Identificeren van minimaal benodigde hoeveelheid metingen per indicator
- Met een beperkt aantal metingen (steekproef) toch uitspraken over ‘alle data’ (populatie) kunnen maken
Formules en voorbeelden
Soms kom je de ‘30-300-regel’ tegen: gebruik n≥ 30 (data continu) en n ≥ 300 (data discreet). Je kunt soms met minder uit. Twijfel je nog, of zijn de belangen groot, kijk dan ook naar de formules en voorbeelden op de volgende pagina. Bij deze formules heb je vaak plezier van een expert: kan een ingenieur, een 6S Master Black Belt of een toegepast statisticus zijn.
Een gangbare formule voor de steekproefgrootte bij discrete data is:
![]() waarbij
waarbij
- 1,96 de waarde is voor een 95% betrouwbaarheidinterval (gangbaar)
- p de geschatte proportie (kans) is dat er een ‘defect’ of ‘juiste’ waarde optreedt
- Δ de helft is van de foutmarge (onbetrouwbaarheid of ‘95% betrouwbaarheidsinterval’)
- n de vereiste steekproefgrootte
Voorbeeld 1. Bij p =0,5 en Δ =0,1 (+/- 10%) is de vereiste minimale steekproefgrootte n= 96 (zeg n =100). Anders gezegd: als uit een steekproef 50 uit 100 tellingen ‘goed’ zijn, ligt het op populatieniveau –voor 95% zeker- tussen p =0,4 en p =0,6 (+/- 10% onbetrouwbaarheid)
Voorbeeld 2. Als in een steekproef 5 uit 10 ‘goed’ zijn, ligt de populatiewaarde -voor 95% zeker- tussen de 19% en 81% (+/- 31% onbetrouwbaarheid (!))
Een gangbare formule voor de steekproefgrootte bij continue data is:
![]() met s nog als standaardafwijking
met s nog als standaardafwijking
Voorbeeld 1. Bij s =10 en Δ =0,05 (+/- 5%) is de vereiste minimale steekproefgrootte n = 5. Anders gezegd: een gemiddelde lengte van Nederlandse mannen van 180 cm uit een steekproef van n=5 met s =10 cm, ligt op populatieniveau (alle Nederlandse mannen) tussen 171 cm en 189 cm (+/- 5%).
Voorbeeld 2. Zie voorbeeld 1, waarbij n=100 een onbetrouwbaarheid van +/- 2 cm ofwel +/- 1% oplevert.
De centrale limietstelling
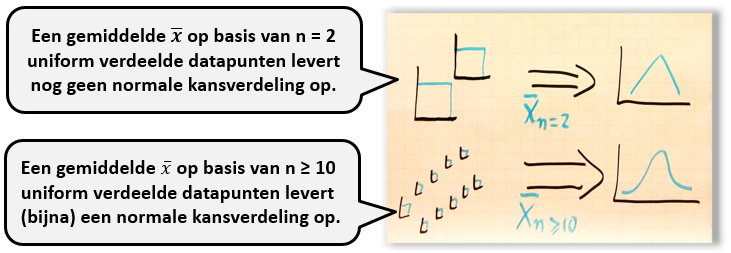
De centrale limietstelling is een natuurkundige wet: ongeacht de kansverdeling van een variabele of indicator x, convergeert de kansverdeling van de som van meerdere x’en of het gemiddelde x ̅ ervan, altijd naar een normale kansverdeling.
Een gemiddelde x ̅ is normaal verdeeld. Als je een normaal verdeeld gemiddelde wilt krijgen is het altijd voldoende om het gemiddelde te nemen van n> 30 metingen. Voor sommaties (optellingen) geldt hetzelfde. Vaak krijg je een normaal verdeeld gemiddelde zelfs al met veel kleinere aantallen, bijvoorbeeld met n=10 (zie hieronder).
Het bewijs van de centrale limietstelling laten wij hier achterwege. Praktisch toets je eerst of data (zeg variabele x) normaal verdeeld zijn. Zo niet, dan kun je met bijvoorbeeld dag- of weekgemiddeldes alsnog statistische analyses maken, uitgaande van normaliteit.
Synoniem van de centrale limietstelling
De centrale limietstelling wordt in het Engels Central Limit Theorem (CLT) genoemd.