Beschrijvende statistiek, zoals een gemiddelde, kan je doen glimlachen. Als je dit artikel helemaal doorleest zonder éénmaal te glimlachen of te lachen, dan beloof ik dat je een compensatiekado krijgt (zie contactgegevens hieronder). Bijvoorbeeld een boekje wat deels over statistiek gaat.
Hoe vaak lacht een mens per dag? Enig idee? Kinderen lachen wel 400 keer per dag, volwassenen gemiddeld vijftien keer.
Aanvullend op hoe vaak, hoe lang (in seconden) duurt zo een lach dan? Ik las net dat de afgelopen decennia we van twintig minuten na de oorlog tot nog maar 6 minuten per dag lachen.
Oeps, terwijl ik heb geleerd dat minstens 10 minuten per dag lachen gezond is.
Ik ben er op gaan letten vandaag. Mijn collega’s lachen vandaag regelmatig enkele seconden lang. Zeg 3 seconden. Soms wel meer dan 10 seconden, maar veel vaker 3 tot 5 seconden.
Schaterlachen kan nog langer duren. Lang lachen, zeg 10+ seconden, komt in mijn omgeving niet vaak voor. Alleen als ik onbewust iets ‘ouds’ zeg, zoals een ‘Twix’ vandaag toevallig een ‘Raider’ noem (‘Twix’ heette tot 1991 of 1992 ‘Raider’).
Of als ik weer eens een schrikreactie zie als ik een Nederlandse vertaling in Engeland geef: “We are hanging on your lips”. Gelukkig kon ze erom (glim)lachen, toen ik mijn taalslordigheid toelichtte. De rest van de Britten vond het gelukkig (ook) grappig.
Of als ik weer eens twee gezegdes, samensmelt tot één. “Te laat achter het net vissen”, bijvoorbeeld. Vond een vis-expert heel grappig. Gezien het gemiddelde aantal keren per dag, denk ik dat er bij mij meer dan genoeg lach-kansen zijn. Dat troost me dan. Dat dan weer wel 😉.
Waarom is het concreet maken van ervaringen in getallen interessant? Ook thuis?
“Meten is weten” is de beroemde uitdrukking. Misschien nog beter, is te beseffen dat door te meten, we meer weten. Zo is de uitdrukking oorspronkelijk ook bedoeld, hoop ik.
Terug naar ons lachen. Hoe vaak en hoeveel minuten lacht u (of jij) per dag? Minstens tien minuten schijnt erg gezond te zijn, of om aan te geven dat je geen depressie of burn-out hebt? Wel eens de duur van je eigen lach gemeten? De meeste mensen weten dit niet echt, en gaan dan wat roepen. In de adviesbranche heet dat wel eens vriendelijk: ‘een indicatie’. Een andere uitdrukking is: “gissen is missen”.
Een gelukkig goed eindigend, persoonlijk voorbeeld. Thuis:
Mijn lieve vrouw, toentertijd mijn vriendin, was eens goed boos op mij toen ik na het werken, in haar ogen, wederom laat thuiskwam. We woonden net samen. “Je bent weer te laat thuis. Sterker, je bent bijna ALTIJD te laat. Dat is toch niet leuk zo?” Ik dacht toen -in mijn onwetendheid- dat ze (flink) overdreef.
Dat valt toch wel mee? Dacht ik.
Maar, ik ben het ‘te laat komen’ toen toch meteen gaan definiëren en meten. “Schat: wanneer ben ik volgens jou … op tijd?” Ze was even stil. “Voor het avondeten, zeg max. om 19 uur”. Ok. “Turven maar”, zei ik als geboren Drenth met een glimlach. Ze keek mij ietwat glimlachend aan.
Na twee weken viel mij op: ik was elke werkdag inderdaad (ruim) na zeven uur thuis. Tot mijn toch wel ‘stomme verbazing’ … ze had gelijk! Ik was doordeweeks altijd te laat thuis.
Toch wel wat confronterend. ‘Gissen’ was hier letterlijk ‘missen’. En misschien wel het missen van mijn grootste liefde. Erg leerzaam. Ik gaf toen tegelijkertijd een training in Six Sigma. Vandaar misschien mijn wat ongebruikelijke ‘meten-is-weten’ aanpak ofwel ‘interventie’ (zoals psychologen dat noemen).
Maar mijn ogen gingen, door het turven van wel/ niet ‘op tijd’ thuis, wel open. Meten is niet alleen ter controle. Meten is dus ook … om te leren. Om te weten. En van daaruit (verder) verbeteren. Later is ze ook nooit meer boos geworden hierover. Logisch, want ik heb daarop mijn aankomsttijd doordeweeks wat aangepast.
In de sport is dit ook meer en meer gewoon. Werken met statistieken om (nog) beter te worden. Zoals in de film Moneyball. Zoals ook in de Atletiek of met je smartwatch tijdens hardlopen. Ja, tegenwoordig is ‘Moneyball’ zelfs in de toch wat conservatieve voetbalwereld gangbaar, nu we de VAR enzo hebben.
Beschrijvende statistiek: de basis van ‘meten is weten’
Veel statistieken, zoals aantallen turven, orde grootte duiden (centrummaten) heet samengevat ‘beschrijvende statistiek’. Je hebt complexere statistiek, zoals werken met kansberekeningen en het formeel toetsen van aannames of hypothesen. Dat is meer ‘analyserend’ dan ‘beschrijvend’. Denk aan onze blog over ANOVA bijvoorbeeld.
Hier richten we ons nu op een intro van beschrijvende statistiek: het bepalen van de orde grootte van, bijvoorbeeld, hoe vaak je lacht.
Een ‘orde grootte’ kan in getallen worden weergegeven. In de statistiek noemen we dit kengetallen of centrummaten. Misschien het bekendste voorbeeld hiervan is het berekenen van het gemiddelde. Maar je hebt ook de mediaan en de modus. Zie hierover nu meer.
Wat is het gemiddelde? En hoe bereken je het gemiddelde?
Het gemiddelde is de som van alle uitkomsten, en dat delen door het aantal uitkomsten. Een voorbeeld van collega Vincent is hieronder gegeven.
Het aantal keren dat Vincent lacht, is hier op 5 werkdagen gemeten. Zie de tabel hieronder.
Tabel 1. Aantal keren gelachen door Vincent tijdens 5 werkdagen*
|
Maandag |
Dinsdag |
Woensdag |
Donderdag |
Vrijdag |
|
13 |
13 |
11 |
12 |
21 |
* Gemeten door kamergenoot Casper, die minstens 7 uren per werkdag bij hem was
Het gemiddelde is dus tweeledig: eerst optellen en daarna delen door het aantal. De som van alle 5 de uitkomsten tijdens werk is: 13+13+11+12+21= 70.
Als je 70 deelt door het aantal 5, is het gemiddelde: 70/5= 14. Gemeten tijdens zijn werk.
Misschien dat Vincent in zijn weekeinde juist vaker lacht. Of juist structureel minder.
Wat is de mediaan? Hoe bereken je de mediaan?
De mediaan is de middelste waarde van een gesorteerde dataset. Bij een oneven aantal waarden, zoals het voorbeeld hierboven (5 metingen). Of, bij een even aantal metingen, het gemiddelde van de middelste twee waarden.
Hoe bereken je de mediaan? Simpel. Zie het voorbeeld van bovenstaande tabel. Als je de 5 metingen sorteert op basis van grootte, krijg je: 11, 12, 13, 13, 21. Zie de onderstaande tabel.
|
Aantal keren dat Vincent lacht tijdens zijn werkdag in een werkweek (gesorteerd naar grootte) |
|
11 (is: kleinste waarde) |
|
12 |
|
13 (is: de mediaan) |
|
13 |
|
21 (is: grootste waarde) |
Het is een oneven aantal, dus de middelste waarde voor wat betreft grootte, ofwel de mediaan, is 13 keer. Als er nog een extra maandag bij zat met waarde 15 van de week erop, dan zou de mediaan worden, op basis van 6 metingen: 11, 12, 13, 13, 15, 21.
Als je dan de middelste 2 waarden van de gesorteerde waarden eruit haalt, krijg je: 13 en 13. Deze optellen levert: 13+13=26. Het middelen van deze twee waarden is uiteindelijk delen door 2. Oftewel: 26/2 =13. Hier misschien wat overdreven, maar dan weet je hoe je daar toe komt. Of hoe een statistische applicatie dit voor je berekent.
Wat is de modus? En hoe bepaal je de modus?
De modus is de meest voorkomende waarde. De term ‘Jan Modaal’ bijvoorbeeld, komt van de orde grootte ‘modus’. Grafisch gezien is de modus de ‘grootste stuk van de taart’.
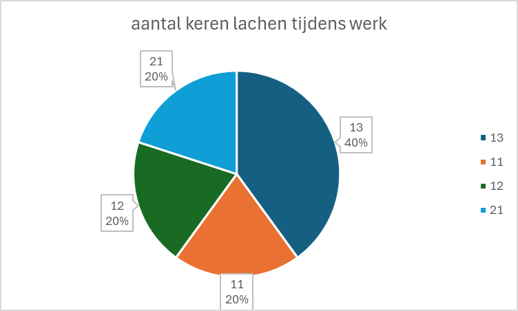
Hoe bereken je de modus? Dat doe je door het meest voorkomende uit een dataset te halen. Hier is dat wederom: 13. Deze komt namelijk 2 keer van de 5 voor in de gemeten week.
In procenten uitgedrukt: 2/5*100=40%. Vandaar de 40% bij de afbeelding bij 13 keer. Op zich is het aantal metingen voor percentages eerlijk gezegd te klein voor nauwkeurige conclusies, maar het gaat hier enkel om te oefenen. Weten hoe groot een steekproef dient te zijn? Lees dan deze pagina.
Hieronder een overzicht van alle centrummaten:
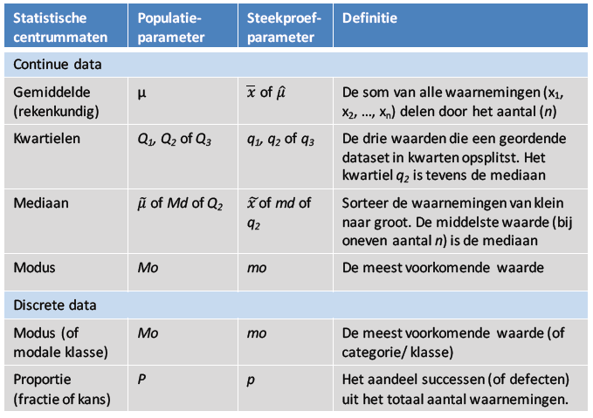
Wanneer is het gemiddelde gelijk aan de mediaan en de modus?
Bovenstaande voorbeeld geeft aan dat het gemiddelde 14 keer is, en de mediaan als de modus 13 keer zijn. Wanneer kies je welke? Dat hoeft dus niet zoveel uit te maken. Maar soms wel.
De eerste tip: kijk verder dan enkel het gemiddelde. Visualiseer de data.
Maak van de data een grafische afbeelding. Als je bijvoorbeeld tientallen tot miljoenen datapunten hebt, zou je een Boxplot kunnen maken. Waarom een grafiek? Nu, als je een Boxplot maakt, zie mogelijk veel uitschieters. Bij uitschieters kan het gemiddelde veel groter uitvallen dan dat deze de ‘orde grootte’ aangeeft. Zeker bij een kleine steekproef, adviseren wij in veel gevallen de mediaan.
Als je werkt met klassen of categorieën, kun je een taartdiagram (een voorbeeld is hierboven weergegeven) of een Pareto-diagram kunnen opstellen. Sowieso, als je met klassen werkt of enkel met namen of, zoals statistici dat noemen, werkt met zogenaamde “discrete data”, ligt de modus voor de hand.
Meer weten over beschrijvende statistiek? Lees dan de uitleg hierover in ons boek online.
 Of koop ons boek: “Lean Six Sigma: Samenzinnig verbeteren”. Dit boek heeft namelijk heel veel statistiek in huis als het gaat om verbeteringen c.q. veranderingen, met name in de grootste hoofdstukken Measure en Analyse. Dit is ons naslagwerk, welke wij in diverse trainingen behandelen.
Of koop ons boek: “Lean Six Sigma: Samenzinnig verbeteren”. Dit boek heeft namelijk heel veel statistiek in huis als het gaat om verbeteringen c.q. veranderingen, met name in de grootste hoofdstukken Measure en Analyse. Dit is ons naslagwerk, welke wij in diverse trainingen behandelen.
Het belang van statistiek voor Organisaties
Het toepassen van goede beschrijvende statistiek op je bedrijfsgegevens biedt talloze voordelen. Niet alleen helpt het bij het identificeren van kostenbesparingen, maar het stelt je ook in staat om strategische beslissingen te nemen. Bovendien kun je met statistieken waardevolle inzichten verkrijgen die je concurrentievoordeel kunnen vergroten.
Door simpelweg de modus, mediaan en gemiddelde te laten zien kun je aanzienlijke verbeteringen realiseren, dit kan zijn in de vorm van besparingen (EUR), minder uren werk of door stappen niet meer te doen die geen waarde toevoegen
Wil je je meer ontwikkelen in statistiek? Volg dan de Lean Six Sigma Green Belt bij LSSP. Of schakel hun hulp in als adviseur voor enkele dagen bij een Management vraagstuk.